How to easily teach computational thinking in your classroom

Many educators across New Zealand are asking the question ‘what is computational thinking’ as they learn to embed the new Digital Technologies | Hangarau Matihiko Curriculum into their class programmes. This blog post will help you learn how to easily teach Computational Thinking (CT) in your classroom using Progress Outcome 1.
Computational Thinking (CT) is a key aspect of the new Digital Technologies | Hangarau Matihiko Curriculum which we provide professional learning to schools and kāhui ako across New Zealand. After breaking down what Computational Thinking (CT) means, staff often realise they are already aligning key aspects of CT in their classes.
The curriculum document provides a clear outline as to where the Computational Thinking Progress Outcomes sit alongside curriculum levels and student year levels.
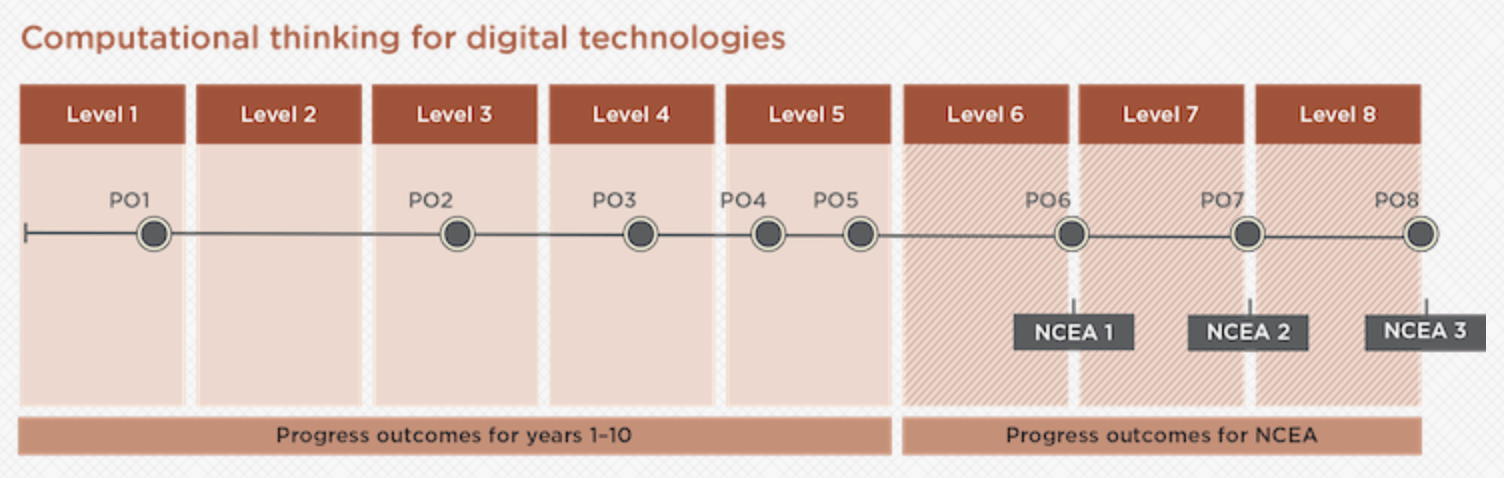
Looking more closely at what teachers already do in their teaching
There are many everyday scenarios teachers can use to illustrate Computational Thinking in action. Click on either of these tabs below to view a primary or secondary example:
This example below is aimed at the second part of Progress Outcome 1.
For example, when a new student arrives into your class you can apply CT to the process for students organising themselves to get ready for the school day, as in this sequence:
- Say ‘good morning’ to your teacher and friends.
- Hanging bag up.
- Get book out of bag
- Take lunchbox to cubby.
- Putting pencil on desk.
- Sit down on mat, etc.
The following day, you ask the new student to go through the process themselves. If they make a ‘mistake’ (where the order is incorrect, or a step missed out) you prompt them with questions as to why they think that order needs to be ‘debugged’. Once the student corrects this, they understand the correct ‘algorithm’ or set of instructions for entering the classroom and getting organised.
Seems easy right?
This is Computational Thinking Progress Outcome 1 from the Curriculum Document:
- Students break down a simple non-computerised task into a set of precise, unambiguous, step by step instructions (algorithmic thinking).
- They are able to give these instructions, and identify if they have gone wrong and correct them (simple debugging).
- By doing this they show that they can use their decomposition skills to take a task and break it down into its smallest steps.
Can you see where the (very basic) example above indicates each bullet point for Progress Outcome 1? Can you also see the links to learning opportunities within the Key Competencies for the New Zealand Curriculum?
Let’s have a look at another example using images. A young student could be asked to move these images into the correct order:
Are they already in the correct order? A young student will realise which one goes on first, second and will be able to articulate why the order is important. This is PO1 – sequencing.
The new Digital Technologies Curriculum doesn’t have to be scary! In fact, you are probably already meeting some of the Progress Outcomes and using computational thinking and haven’t yet made the links in your practice. We demystify the DTC and make the links obvious so you can transfer this exciting new curriculum area into your programme with ease.
This example below is aimed at the second part of Progress Outcome 4,
Students understand that digital devices represent data with binary digits and have ways of detecting errors in data storage and transmission.
Firstly, we look at binary which is Progress Outcome 3:
Binary is the language of technology. Information is stored in hardware as either a transistor which is on or off. We need to use our abstraction skills to think how this can be represented: hardware (the transistors) needs to translate this into what the computer is actually ‘reading’. This means, the information is given in 1’s and 0’s. 1 = on and 0 = off.
Let’s break this down further:

If the binary digit is 0, the transistor is off, so we don’t count it for the total.
This example above = 65. Because the binary digit above 64 is 1 (on) as well as the binary digital above the 1. Both are ‘on’ so we count them together which totals 65.

Even cooler, is that this particular combination represents a capital A. So whenever you type ‘A’ somewhere on a device, there is a row of 8 transistors in this pattern.
Now, we have done a very quick introduction into binary, we can complete a Progress Outcome 4 activity on how to detect errors in binary code.
Activity:
- Have 64 cards which are two different colours on either side. I’ve used black and white for this example (this could also be drawn on the board or printed on a handout).
- Ask students to arrange the cards randomly black and white in a grid 8 x 8

- Add an extra column and row to the grid:

- Add a parity bit (a black square) onto each row and column that has an odd number of black squares.
A parity bit, is a single bit added to a binary code. It is either 1 (on) or 0 (off) to make the total number of 1 bits either even (“even parity”) or odd (“odd parity”). Main task
Main task - Can you flip one card inside the red lines (eg. not the parity bits you have added) and see if a buddy can work out the pattern and decide where there is an error using the parity bits?
What you are trying to find
If the rows have an even number of black squares, the parity is white. If the row has an odd number of black squares, the parity bit is black. Same with the columns.
Once students see there is an irregularity in a row, they must find the irregularity in the columns. Where the rows and columns intersect is where the binary digit is incorrect.
This means that students can use this logic to find where there is an error in the code. This is essentially what a computer does to find where there is a ‘bug’ in the binary code.
Key questions:
- Can the students relate the black/white cards to what this means in binary?
- Can students write out what the cards randomly placed would mean in binary?
- Can students explain what a parity bit is for? And how it works?
- Why is this checking system important for technology?
So how does this activity relate to PO4?
Students understand that digital devices represent data with binary digits and have ways of detecting errors in data storage and transmission.
Get PDF examples of these progress outcomes:









 Main task
Main task
Facebook Comments